Learning AI (and nuclear physics) Poorly: Sunday Friendsgiving Shenanigans

(originally posted to LinkedIn)

Our friend group got together on Sunday and the kids were in town. I sat next to one of them who is going for a PhD in Nuclear Physics and we got to talking about his lab and the work they do. Super interesting stuff but he made a critical mistake by asking, “Do you know anything about AI or ML? We’d like to explore using it.”

Oh sweet summer child…

I am sure he regrets asking that question, but I learned a lot and even went home and dug in to write this post talking about how one might use neural networks to help solve nuclear physics problems.

(Spoiler alert: I have no idea!)

Nuclear Physics Explained Poorly #

From what I could figure out, his research revolves around building models to predict what happens inside nuclear reactors at the atomic level. They use Monte Carlo methods (see my previous post Learning Monte Carlo Methods Poorly: Randomly Find π by Throwing Yard Darts) with about 7 different variables (energy, spin, scatter, etc.) to calculate how neutrons behave while flying through something like a hunk of plutonium over time.

Not super exciting… but it could be if you frame the problem around the development of the nuclear bomb. I’m taking a bit of a risk here because I haven’t had the chance to watch Oppenheimer. Instead, I found the paper Neutronics Calculation Advances at Los Alamos: Manhattan Project to Monte Carlo which I’m sure is way less entertaining than the film, but super interesting from a computation viewpoint.

Nuclear Fission and Chain Reactions #

In the early 1930’s, scientists learned that if you bombard a large, heavy atom (like uranium) with neutrons there’s a chance that one will hit the nucleus and split the atom apart releasing a ton of energy and particles including neutrons. There’a a chance those neutrons flying out of the split atom will hit other atoms, splitting those apart. They figured that this could go on and on in a chain reaction that would release an earth shattering kaboom.

Of course, that was only a theory until Enrico Fermi, Frederic Joliot, and Leo Szilard independently observed neutrons flying out of split atoms. At that point, they had to figure out how to get those neutrons to reliably hit the nucleus of nearby atoms to enable a chain reaction.

Shape Matters #

To do that, scientists began developing equations to characterize the energy released by a chain reaction, but they assumed a perfect arrangement of atoms in a perfect sphere (Assume a spherical cow in a vacuum) which obviously won’t work IRL. The equations evolved into the “Neutron Transport Equation” which is is a bananas crazy complicated formula that describes a neutron’s movement through material. It was too hard to use so they developed “Neutron Diffusion Theory” as an approximation that people could actually use to calculate answers. In fact, Los Alamos created the “T-5 Desktop Calculator Group” which was almost exclusively women who would hand compute segments of a calculation and pass the results to the next person for further calculation (like a human GPU?)

The whole point was to figure out how much fissionable material was necessary and how it should be shaped to enable a near instant nuclear chain reaction that would lead to a massive explosion. And, I guess, we all know now how that worked out.

It is All About Predicting the Neutron’s Path #

If you’re not asleep yet, you’ll see that a lot of this work is about predicting where and how these neutrons are flying around inside some material. Initially, they were solving mathematical equations that predicted these things. However, around 1947 the “Monte Carlo Method” was invented by Stanislaw Ulam. It is a method to solve complex problems using random sampling… kind of calculating the average or probable behaviors of variables inside a system by observing the outcomes of a large number of experiments… So, instead of doing the math, you’re taking measurements and calculating the most likely solution (so… you get a range of values and the likelihood of that number being correct instead of the one, solid, correct number.)

Scientists at Los Alamos used this technique to estimate the probable flight path of each neutron flying out of a split atom based on the exact collision point of the initial neutron. Then for each of those neutrons estimate the chance of them hitting another atom and splitting it. It looked like this:

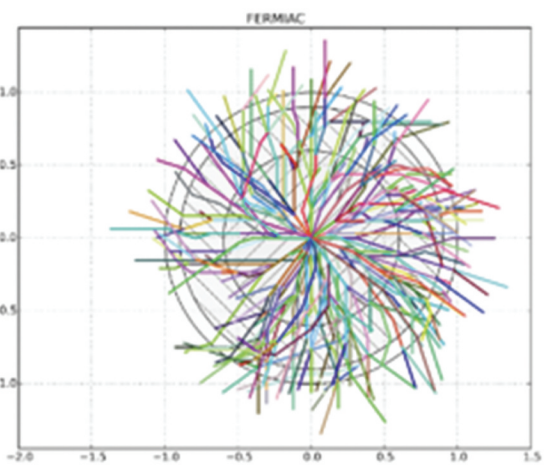
That drawing was generated by an mechanical computer made out of brass rollers called FERMIAC that was used until the lab was able to get time on ENIAC, the first programmable electronic computer. Von Neumann did the planning to create the monte carlo algorithm to solve the neutron transport problem on the ENIAC machine. Being able to calculate these paths quickly was wildly successful. From the paper cited above:

The algorithm used for the ENIAC was similar in many respects to present-day Monte Carlo neutronics codes. Some example similarities are reading the neutron’s characteristics, finding its velocity, calculating the distance to boundary, calculating the neutron cross section, determining if the neutron reached time census, calculating the distance to collision, determining if the neutron escaped, refreshing the random number, and determining the collision type. A card would be punched at the end of each neutron history and the main loop restarted. The neutron history punched cards were then subjected to a variety of statistical analyses.

What’s Happening Today? #

So, obviously, the physicists at Los Alamos did amazing work and a lot of development and advancements have happened through the years but I was kind of shocked that cutting edge PhD work (at least in my friend’s case) is still based on Monte Carlo methods.

I won’t pretend like I know anything about nuclear physics but I do know that monte carlo methods are used heavily in machine learning. For example, in setting up initial hyperparameters (the values we define before any training even starts like activation function, loss functions, etc.)

Does it make sense to flip the problem upside down and use machine learning techniques to optimize portions of the monte carlo process? Can we use trained models, for example, to speed up computation while running nuclear physics simulations?

Like the spoiler said… I have no idea.