Learning AI Poorly: Training AI to Pick a Number Between 1 and 10

(originally posted on LinkedIn)

Every time I type, “and then you train the model” I stop and think to myself, “Can I explain that?” and… well… No, I can’t. Not without a lot of big words and tedious math. So, I gloss over it. Save it for another day.

Can’t put it off any longer. Today is the day we talk about training but we are going to do it in easy mode and ignore a lot of details. We will use Tensorflow at a pretty low level to define a model inspired by a game at a shady casino Cousin Eddie found and then we will train it to do something… All without using any big words or crazy math. The code will be kind of hard to read but hopefully the concept of training a model will make sense.

What is happening when you “train” a model? #

Ok, so you have this thing called an Model that takes some input (almost always a set of numbers) and it generates some output (almost always another set of numbers.) If you are lucky, the numbers you get out of it make sense in some sort of magical way. For, example, if you give it numbers that represent the phrase “A picture of Clark Griswold and Cousin Eddie in a casino” maybe it will output pixel data that looks like the picture at the top of this article. That would be great! Magic even.

A model contains a “neural network” which is kind of like a bunch of little calculators that are connected together. Each calculator has a formula in it (usually, the slope-intercept equation of a straight line, Y = mX + b)* The calculator takes in a number, X, outputs the answer, Y, and sends that number to the next calculator down the line. The calculators can be connected together in layers like this:

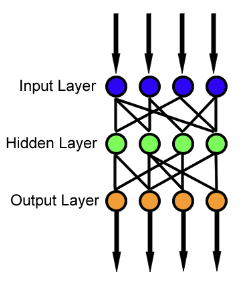
Can we do that ourselves without getting bogged down in a lot of details? I think so.

In the 1997 American comedy film, National Lampoon’s Vegas Vacation, Clark Griswold wound up at the Mirage casino where he gambled away his family’s savings. Cousin Eddie came to the rescue by taking him to an off-strip casino that had more manageable games like Rock Paper Scissors, Coin Toss, Guess Which Hand, and of course my favorite, Pick a Number Between 1 and 10. It didn’t end well.

I bring that movie up because neural network training is like playing Baccarat at the Mirage… Baccarat is really tedious and annoying, much like AI. In real AI models, there are billions of m’s and b’s to update and everything is connected in wacky ways. Like the Mirage, it is no place for beginners.

But! If training a neural network is just having it guess the right m’s and b’s for a bunch of Y=mX+b equations, can we take a baby step and make a neural network with just one calculator with one variable that adjusts itself via training? Can we train it until it outputs a specific number? Sure! Can we say that we built an AI that plays the “Pick a Number Between 1 and 10” game? Why the hell not?

While we are at it, let’s use Tensforflow to do it. This is total overkill but you might as well see some real code.

Ok, here’s what we are doing to create a “pick a number” Tensorflow model: 1) 2) Create a “Model” with one “Variable” that starts out as some sort of random number. The output of the model is just the value of this variable. It ignores all input. 2) Train the model until it is able to output the number “7” using these steps: give it a random number for input but always give it “7” as the output adjust the variable in the model so it outputs something a little bit closer to “7” repeat a bunch of times until you’re satisfied that the model will return 7 consistently. 3) Give the model a random number and see if it outputs something close to “7” Got it? Let’s go. Open up a fresh google colab notebook and paste this:

import tensorflow as tf
import matplotlib.pyplot as plt
import random

That sets up your libraries (code you want to use that someone real smart wrote and tested). Now, paste this to create a Tensorflow model:

class SimpleMod(tf.Module):
  def __init__(self, **kwargs):
    super().__init__(**kwargs)

    # This is the variable we are going to "train"
    self.answer = tf.Variable(random.uniform(1,10))

  def __call__(self, x):
    return self.answer
    
simple_model = SimpleMod()

That’s the minimal code needed for a Tensorflow model. (They’re called Modules instead of models but whatever.) The model contains one variable I called “self.answer” and when you “call” the model it just returns the value of that variable. We set the initial value of “self.answer” to a random number between 1 and 10. That means when this model starts out, it will have no idea what number to guess. It will just output a random number. It’ll need to be trained.

def simple_loss(target_answer, predicted_answer):
  return tf.reduce_mean(tf.square(target_answer - predicted_answer))

Here’s the function that uses that loss function to train your model:

def simple_train(s_model, guess, answer, learning_rate):

  with tf.GradientTape() as t:
    # current_loss is where the model is at this moment.
    current_loss = simple_loss(answer, s_model(guess))

  # d_answer is the gradient delta between the answer and the loss...
  # we don't discuss gradients here... we just smile and nod
  d_answer = t.gradient(current_loss, s_model.answer)

  # Update the model's "answer" variable to be closer to the number we want
  s_model.answer.assign_sub(learning_rate * d_answer) 

This function adjusts the “self.answer” variable inside the model. That’s training! To do that:

• It runs the current model against a piece of test data using the function call “s_model(guess)”
• It compares the output from the model to the correct “answer” (which is always 7) using the loss function and saves that in a temp variable called current_loss: “current_loss = simple_loss(answer, s_model(guess))”
• It uses a thing called a gradient (complicated concept with calculus, feel free to gloss over this) to figure out how to slowly inch the model closer to the correct answer. To do that, it calculates the gradient based on the current_loss and the model’s current internal variable. The output of the gradient calculation is a small value that we can use to inch our model closer to giving the correct answer
• Finally, we adjust our model by updating it’s internal value for self.answer using the gradient (a push toward the right direction) and a small number we call “learning_rate” which further slows down the pushes. Don’t want to over do it.

Ok, so that’s the training step. We need to run that a bunch of times against some training data. So, paste this training loop:

# Collect the history of answers to plot later
answers = []
epochs = range(20)  

def simple_training_loop(s_model, answer, guess):

  for epoch in epochs:
    # Update the model with the single giant batch
    simple_train(s_model, guess, answer, learning_rate=0.1)

    # Track the model's answer before we update it
    answers.append(s_model.answer.numpy()) 

That code will train the model 20 times (epochs) for each number in a training set. It also keeps track of the internal value of the model so we can watch it get closer to the real number while training. Let’s make some data and actually train the thing:

NUM_EXAMPLES = 205

# A vector of random values between 0 and 10 to give to the model
guesses = tf.cast(tf.linspace(0, 10, NUM_EXAMPLES), tf.float32)

# a vector of 7's
the_number = tf.cast(tf.linspace(7.0, 7.0, NUM_EXAMPLES), tf.float32)

# run it!
simple_training_loop(simple_model, the_number, guesses)

That code generates 205 data points to train. Remember, we pass random numbers to the model but always expect “7” as the output. So, we generate a list of 205 random numbers and a list of 205 7’s. Then we run the training loop.

Side Note - Tensorflow is designed to work on long lists of numbers, or vectors, in parallel. That’s necessary when working with millions of variables, but obviously overkill in this example. But, since that’s how it works it kind of hides the fact that each of the 205 samples in our data get pushed through training 20 times… We’re working in vectors, not individual loops so that’s weird… that’s also why everything is wrapped with tf.* datatypes. They’re all vectorized. Let’s just smile, nod, and keep reading…

Ok, so if you ran all that code, you just trained your model to guess the number 7. Remember how we saved the state of the model to see it get closer to the number 7? We can plot that.

plt.plot(answers)
plt.title(f"training to guess {the_number[0]}, last guess was {answers[-1]}")

Here’s what it looked like one time I ran it:

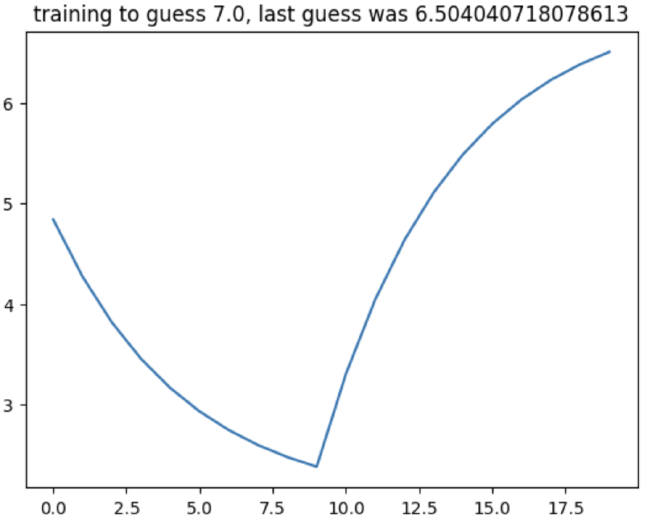
What happened is the model was randomly initialized to something like 4.85. The first few steps of training caused the variable to go the wrong way for a bit, but then it quickly recovered and got to 6.5… That’s close! It learned! (sort of) And, if you change epochs from 20 to something like 50 or 100, the line will get very close to 7. Here’s 100 training steps:

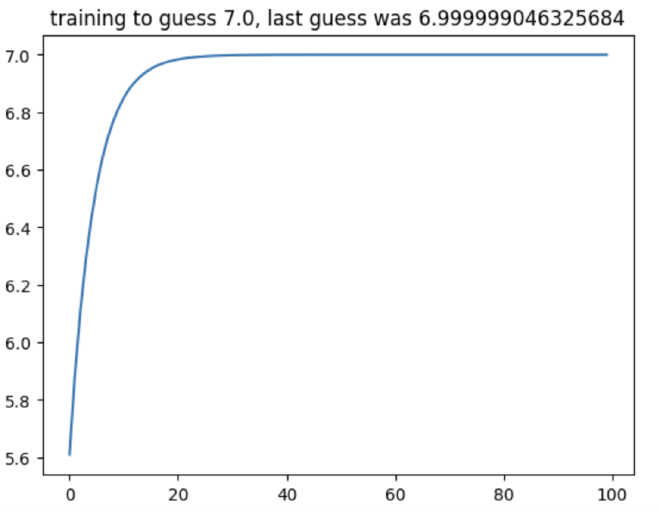
Does it work? #

That’s easy, you can use the model and print out the result by simply typing:

print(simple_model(8.0))

That outputs something like:

<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=6.999999>

Which looks crazy, but remember we are in Tensorflow land and everything is a wacky thing called a tensor. The actual value is that “numpy” thing which is 6.999999999. I’d say it works. You can re-run that code with any number and the model will always return 6.99999999 because that’s how we built and trained it.

Congrats! You used real Tensorflow code to build and train a model to get the output you wanted. Great job. Who’s ready to go to the Mirage?

• You ever hear people mention weights and biases in neural networks? Weights sort of are the slope and bias is sort of the y intercept. So, while I write y = mx + b (slope intercept) you’ll usually see it written as Y = Σ(weight • input) + bias in a ML/AI context. Notice that summation, remember how I said Tensorflow is optimized to work on vectors in parallel? That’s why.